※クリックで全体表示。
|
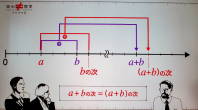
『笑わない数学』【↓の記事参照】の加法の定義のところでは、0から始まる数直線上のaとbについて加法の定義が説明されていたが、私が理解する限りでは、aやbはあくまで順番であって、等間隔の目盛の上に配置される必要はないように思われる。
|
|
Copyright(C)長谷川芳典 |
※クリックで全体表示。

|
『笑わない数学』【↓の記事参照】の加法の定義のところでは、0から始まる数直線上のaとbについて加法の定義が説明されていたが、私が理解する限りでは、aやbはあくまで順番であって、等間隔の目盛の上に配置される必要はないように思われる。
|
【連載】笑わない数学(6)『1+1=2』(5)「1×1=1」「2×2=4」の証明 昨日に続いて、10月18日にNHK総合で初回放送された、『笑わない数学 シーズン2』: ●1+1=2 についてのメモと感想。 今回は前日のところで言及した乗法の定義についてもう少し考えてみることにしたい。 Bingは、乗法の定義は以下のように定義していた。なおこの日記では、後者を意味するS()はsuc()と表記しておく。 ペアノの公理に基づいて乗法を定義する場合、自然数nとmの積n×mは、以下のように再帰的に定義されます:ウィキペディアでも同様に定義されていた。 この定義は分かりやすく言えば、
もっとも上記のような例え話では、我々が日常生活場面で使っている足し算やわり算の常識が邪魔をして、暗黙の前提が入り込む恐れがある。 そういう意味では、+とか×といった記号を使わず、「+の代わりに◆」、「×の代わりに★」といった暗黙の前提が入りにくい記号に置き換えて考えたほうがかえって分かりやすくなる。 その場合、乗法は、
ここで興味深いのは、単位元1は、特別に定義しなくても、上記の「n★0=0」と「n★suc(m)=n★m◆n」という乗法の定義から自動的に証明できるということである。但しこれは私が独自に行った証明によるものであり、どこかでミスを犯している可能性はある。念のためBingに尋ねたところ、 「1×1=1」を証明するには、ペアノの公理と乗法の定義を用いて、以下のように証明することができます :という回答をいただいた。私自身が行った証明と同じロジックになっているので一安心。 Bingにはついでに「2×2=4」も証明してもらった。 「2×2=4」を証明するには、ペアノの公理と乗法の定義を用いて、以下のように証明することができます :なお、Bingでは省略されていたが、「2×2=4」を証明する前にはまず「2」と「4」を定義しておく必要がある。
さらに証明の中で「2+2=4」が使われていることからみて、まずは「1+1=2」、、続いて「2+2=4」を証明しておく必要がありそうだ。 もう1つ興味深いのは、乗法の定義では相変わらず、suc()という「後者」の概念が用いられているだけで「間隔」や「比率」は何も定義されていないことである。乗法というと「何倍?」というような比率がすぐに思い浮かぶが、順序構造だけの世界でも乗法は成り立つということだろうか? なお、今回は0以上の整数(自然数)のみを扱ってきたが、負の数の概念を導入すれば、例えば「(−1)×(−1)=1の証明」というような問題が出てくる。ネット上ではいくつか分かりやすい解説が行われている。 次回に続く。 |