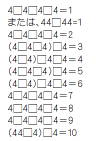【小さな話題】最近視たYouTube動画(数学編)「マルチンゲール法」「梶田光さん」「正多角形」「アインシュタイン問題」「ケプラー予想」
最近視たYouTube動画のメモと感想。今回は数学関係の解説動画から。順不同。
- マルチンゲール法はなぜ破綻するのか
別名『倍々法』とか『倍追い法』と言われている戦略であり、どんなに負けても次の回の掛金を損失金額分まで増やしていけば、いつか勝った時には損失分の2倍が受け取れるため必ず儲かるという方法。しかし、じっさいには、負け続けていく中で倍々に増える掛け金額が膨大になりゲームを続けられなくなってしまうという話。
確率論的には期待値が無限大になるのに、なぜ思惑通りに儲からないのかという話になるが、要するに、こうした賭けは独立試行であって、「過去は負け続けたから今度こそ勝つだろう」という錯覚がもたらしたものと考えればいいのかと思われる。
- 素数の新定理を発見した天才少年がチートすぎる【ゆっくり解説】
数学そのものの話ではないが、2008年生まれの梶田光さん(2008年生まれで現在15歳)は10歳の時に双子素数や完全数に関する研究をしていて新しい定理を発見したというからスゴい。さらに小学生の時に数学の専門書『Mathematics1001』(英文)を3年かかって読破。研究テーマは10歳の時が『スーパー双子素数の個数公式と高橋条件』、13歳の時が『乗数hつきオイラー双子型メルセンヌ超完全数』であった。動画の中では『スーパー双子素数』や『超完全数(スーパー完全数』についても簡単な解説があった。画一的かつ底上げ型の公共教育とは別にギフテッド教育を行う必要、『孫正義育英財団』のしくみが紹介されていた。
- 快挙!高校生が華麗に証明した数学定理【橋本幸治の理系通信】(2023年6月27日)
「円に内接する多角形の中で、正多角形が一番大きな面積を持つことの初等的証明」という興味深い話題。この定理自体はすでに証明されているが、西宮市立西宮高校の生徒4人が新たに初等的な方法で証明し、オーストラリアの大学が発行する数学雑誌「Parabola」に、「注目すべき論文」として掲載されたという話。
リンク先によれば、論文出典は以下の通り。
Rikuto Tanaka, Jinya Miyamoto, Yuki Maruo, Keita Nakayama and Ryohei Miyadera (2023). An elementary proof that the regular polygon is the largest among polygons that are inscribed in a circle. Parabola , 59(1), 1-8.
- 【アインシュタイン問題】50年来の超難問がついに解かれました【ゆっくり解説】
平面充填については2022年7月8日の日記でも取り上げたことがあった
。この時点ではまだ未解決であったがウィキペディアの最新版には以下のような新情報が追加されていた。動画では分かりやすく解説されている。
最初の非周期的タイル張りは、1966年に発見された、20426種類のタイルを使うものである。その後、より少ない種類数のタイルによるタイル張りが発見され、1974年にはイギリスの物理学者ロジャー・ペンローズが非周期的タイル張りの可能な2種類の菱形のタイル「ペンローズ・タイル」を考案したが、非周期的モノタイル(単一で非周期的タイル張り可能なタイル)が存在するかどうかは長らく未解決であり、アインシュタイン問題と呼ばれていた。
しかし、2011年にSocolar?Taylor tileと呼ばれる一種類の非連結なタイルで非周期的タイル張りが可能であることが発見され、2023年にはDavid Smith, Joseph Samuel Myers, Craig S. Kaplan, Chaim Goodman-Straussが、初めは裏返しを使ってもよいという弱い条件のもとで"帽子"("hat")と名付けられた13角形のタイル1種類で非周期的タイル張りが可能であることを報告し、それから間もなく、"帽子"の改良によって裏返しの不要な14角形の非周期的モノタイル「Spectre」を発表してアインシュタイン問題の完全解決に至った。
アインシュタイン問題についてはこちらにより詳しい解説がある。なおここでいう『アインシュタイン』というのはドイツ語のタイル1枚を意味する『ein stein』をもじった名前であり、相対性理論で有名なアインシュタインとは関係ない。
- フェルマーの最終定理を超越した究極の難問「ケプラー予想」とは?【ゆっくり解説】
『ケプラー予想』とは、ケプラーが数学的に予想した「空間を球でいちばん効率よく満たす方法」に関するもの。ウィキペディアでは
1998年にトーマス・C・ヘイルズ(英語版)はラースロー・フェイェシュ=トート(英語版)が提案した方法に従ってケプラー予想を証明したと発表した。多数のケース一つ一つを複雑なコンピュータシミュレーションでチェックするしらみつぶし法(英語版)であった。査読者は証明が正しいことを「99%確信している」と評した。よってケプラー予想は定理として受け入れられる寸前に来ている。2014年、ヘイルズに率いられたフライスペック・プロジェクト(英: the Flyspeck project)のチームは、定理証明支援ツールであるIsabell(英語版)およびHOL Light (英語版)を組み合わせて用いることにより、ケプラー予想の形式的証明を完了したと発表した。
と記されている。リンク先にも記されているように、この問題には実用的価値があり、もともとは、
ケプラーが球の配置を研究し始めたのは、1606年におけるイギリス人数学者・天文学者、トーマス・ハリオットとの文通がきっかけである。ハリオットは友人で雇い主のウォルター・ローリーから船倉に砲弾を効率的に積み込む方法の問題を与えられていた。ハリオットは1591年に様々な積み上げパターンの研究を出版し、さらに進んで初歩的な原子論を発展させた。
ということであった。
|