|
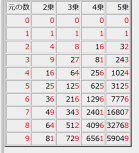
0から9までの整数を2乗〜5乗した時の数と下1ケタの数字【赤字】。下1ケタの数字は4乗すると、0、1、5、6のいずれかとなり、5乗すると元に戻る。下1ケタの数字は、10以上のあらゆる整数(もしくは負の整数)でも同様。1998年5月30日の日記参照。
|
|
Copyright(C)長谷川芳典 |

|
0から9までの整数を2乗〜5乗した時の数と下1ケタの数字【赤字】。下1ケタの数字は4乗すると、0、1、5、6のいずれかとなり、5乗すると元に戻る。下1ケタの数字は、10以上のあらゆる整数(もしくは負の整数)でも同様。1998年5月30日の日記参照。
|
【小さな話題】2021年京大・文系数学の整数問題の拡張(続き) 3月1日の日記で、今年の京大の文系数学の入試問題の1つ、 ●pが素数ならばp4+14は素数でないことを示せ。 という整数問題に言及した。3月1日の日記では、 ●pは自然数である。pが3の倍数でないならばp4+14は3の倍数となる【なので、素数ではない。但しp=3の場合にふれておく必要がある】。 をベースとする解法を示したが、この問題は、 ●pは自然数である。pが5の倍数でないならばp4+14は5の倍数となる【なので、素数ではない。但しp=5の場合にふれておく必要がある】。 をベースにしても解くことができる【鈴木貫太郎さんのYouTube参照】。 鈴木貫太郎さんの解法はmod5の合同式を使った方法であるが、心理学の知り合いの守一雄さんから、以下のような合同式を使わない解法を教えていただいた。 1)素数の下一桁に注目する。要するに、10進法では、2より大きい素数の下1ケタは必ず1、3、7、9のいずれかとなる【2、4、、8、0の時は偶数、5の時は5の倍数なので素数ではない】。これらを4乗すると下1ケタはすべて1となるので、これに4、9、14、19などを加えると、それらの和の下1ケタは必ず、0か5になることが分かる。これをちょっと変更すれば、 【1】5の倍数以外のすべての正の整数は、4乗した値に5m-1(m≧1)を加えると5の倍数になる 【2】5の倍数以外のすべての正の奇数は、4乗した値に10m-1(m≧1)を加えると10の倍数になる ということを示すこともできる。 上記では、4乗した結果に正の整数を加えることになっているが、例えば「4を加える」の代わりに「1を引く」、「【元の入試問題の】14を加える」の代わりに「1を引いて15を加える」としても同じことになる。引き算にすれば、以下のような高校入試向けの問題になりそうだ。 【3】●5以外の自然数を4乗した値から1を引くと、5の倍数になることを証明せよ。 証明としては、まず、 x4-1 =(x2-1)(x2+1) =(x+1)(x-1)(x2+1) =(x+1)(x-1)(x2-4+5) =(x+1)(x-1)[(x+2)(x-2)+5] と因数分解しておく。次に、xの代わりに「5n+1」、「5n-1」、「5n+2」、「5n-2」を入れると、(x+1)、(x-1)、[(x+2)(x-2)+5]のいずれかの部分が5の倍数になるので、それらの積も5の倍数になること[※]が証明できる。 [※]xが奇数の時は、x+1は偶数となるので、積全体も偶数となり、かつ5の倍数であるから、結果として【2】の証明となる。 以上は、高校入試レベルの問題かと思うが、もし、 【4】7以上の素数を4乗した値に9を加えると10の倍数になることを証明せよ。 という問題が出されると、えっ、素数ってf(n)の形では表せないはずなのに【nは整数】、どうしてこんなことになるの?とビックリしてしまうが、「2以外の素数はすべて奇数」と考えれば、上記の【2】に含まれていることに気づくだろう。 余談だが、1998年5月30日の日記に記したように、10進数で表した整数の下1ケタは、5乗すると同じ数字に戻る。6進数で表した場合は、3乗すると元に戻る。もっと一般化して、 ●n進数で表した時は何乗すれば元に戻るか、また元に戻らないのはnがとういう時か? というのが、私が高校生の頃に考えた「循環数(仮称)」の問題であった。ちなみに、今年の岡大の数学入試問題の中に、 ●nが整数のとき,nを6で割った時の余りとn3を6で割ったときの余りは等しいことを示せ。 というのがあったが、これもまた6進数で表した時に下1ケタの数字が同じになるという意味。 |